Schemat wyboru
Jeżeli wybór odpowiedniego testu korelacji stanowi dla Ciebie problem poniżej znajduje się uproszczony schemat wyboru, któru na pewno pomoże Ci w wykonaniu analizy statystycznej do Twojej pracy dyplomowej
Korelacja – co to?
Korelacja to inaczej współwystępowanie. Określa związek pomiędzy zmiennymi. Dzięki korelacji wiemy na pewno, że jeśli A jest większe, to B także wzrasta. Obie zmienne zmieniają się równocześnie. Na przykład:
- wzrost wiąże się z wagą,
- czas poświęcony na naukę wiąże się z wynikiem z egzaminu,
- stres wiąże się z osiągnięciami akademickimi.
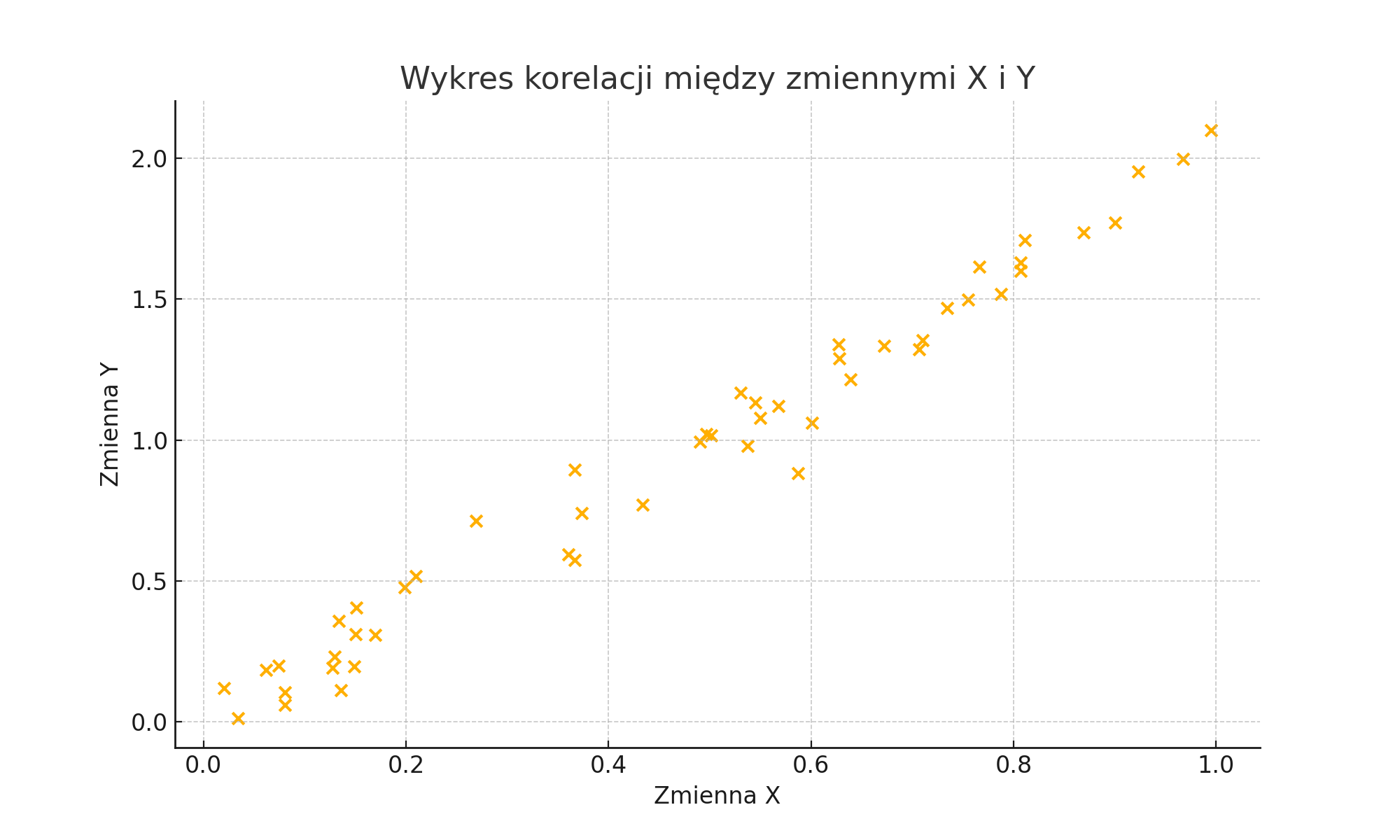
Jak interpretować wynik korelacji?
Siła i kierunek związku
Aby dobrze zinterpretować wartość współczynnika korelacji (wynik) musimy wiedzieć, że może on przyjąć wartość od -1 do 1.
Jeżeli wartość współczynnika jest bliska 1 mówimy o korelacji dodatniej. To znaczy, że jeśli zmienna A ma wartość wysoką – to zmienna B także. Naturalnie jeśli A ma wartość niską – to i B.
Jeżeli wartość współczynnika jest bliska -1 mówimy o korelacji ujemnej. To oznacza sytuację przeciwną: jeśli zmienna A ma wartość wysoką – to zmienna B ma niską. I odwrotnie: jeżeli zmienna A ma wartość niską – to zmienna B ma wysoką.
Im wartość współczynnika jest bliższa 0 mówimy o braku związku liniowego. Należy pamiętać, że pomiędzy tymi zmiennymi może wystąpić inny związek, którego nie da się opisać linią prostą albo może nie być między nimi żadnego związku. Sam wynik korelacji bliski 0 mówi nam tylko o tym, że nie ma związku liniowego. Czyli wysokość zmiennej A nie ma prostego przełożenia na wysokość zmiennej B (dodatniego czy ujemnego).
Wielkość współczynnika
- |r| = 0 – brak korelacji.
- 0 < |r| < 0.3 – bardzo słaba korelacja.
- 0.3 ≤ |r| < 0.5 – słaba korelacja.
- 0.5 ≤ |r| < 0.7 – umiarkowana korelacja.
- 0.7 ≤ |r| < 0.9 – silna korelacja.
- 0.9 ≤ |r| ≤ 1 – bardzo silna korelacja.
Wartości współczynnika korelacji są interpretowane różnie w zależności od dziedziny nauki. W psychologii oraz naukach społecznych korelacje powyżej 0.3 są często uważane za istotne, ponieważ zmienne ludzkie rzadko są ze sobą silnie skorelowane. W naukach przyrodniczych i technicznych często oczekuje się wyższych wartości, aby uznać korelację za istotną.
Istostność korelacji
Podczas interpretacji korelacji istotne jest także sprawdzenie, czy wartość korelacji jest statystycznie istotna. Wartość p (np. p < 0.05) wskazuje, czy obserwowana korelacja mogła wystąpić przypadkowo. Jeśli wartość p jest niska (np. poniżej 0.05), można uznać korelację za statystycznie istotną, co oznacza, że istnieje małe prawdopodobieństwo, iż zaobserwowana zależność jest przypadkowa.
Oczywiście mowa tutaj o dobrze wszystkim znanym p < 0,05 czyli istotności testu. Wskazana wartość (0,05) jest wykorzystywana powszechnie i najprawdopodobniej będziesz miał z nią styczność podczas pisania Twojej pracy dyplomowej dyplomowej.
A czy wiesz, co oznacza?
Wartość p informuje nas, że z jakim prawdopodobieństwem nasz wynik jest dziełem przypadku. Czyli jeżeli nasze p = 0,05 to istnieje 5% prawdopodobieństwa, że uzyskane wyniki są przypadkowe oraz 95%, że są wynikają z rzeczywistego związku między zmiennymi.
Korelacja pozorna
Bardzo ważnym jest, aby dobrze zastanowić się przy interpretacji wyniku. Może się bowiem zdarzyć, że stwierdzimy zależność, która w rzeczywistości nie istnieje.
Bardzo znanym przykładem korelacji pozornej jest stwierdzenie zależności pomiędzy ilością bocianów a ilością dzieci, które urodziły się w danym regionie.
Ha! Rzeczywiście taki związek występuje. W rzeczywistości liczba bocianów i liczba dzieci są powiązane z cechami obszarów wiejskich, gdzie często obserwuje się zarówno więcej bocianów, jak i wyższy wskaźnik urodzeń, ale nie ma między nimi bezpośredniego związku.
Inny ciekawy przykład to wzrost sprzedaży lodów skorelowany ze wzrostem liczby utonięć.
Wyjaśnienie: W rzeczywistości obie te zmienne są powiązane z temperaturą. W cieplejsze dni ludzie chętniej kupują lody i częściej wybierają się nad wodę, co może prowadzić do większej liczby utonięć. Temperatura jest tutaj zmienną ukrytą.
Korelacja ≠ wpływ
Bardzo często zdarza się, że stawiając hipotezy studenci piszą „wpływ” a mają na myśli związek. Lub – co gorsza – naprawdę sądzą, że wynik korelacji świadczy o wpływie. Pamiętaj, że naprawdę tak nie jest. Istnienie korelacji pomiędzy zmiennymi mówi nam tylko tyle, że wartości tych zmiennych są ze sobą związane.
Przykład: Związek między stresem a zdrowiem psychicznym
Wiele badań pokazuje, że istnieje silny związek między poziomem stresu a zdrowiem psychicznym, np. depresją czy lękiem.
Wyjaśnienie: nie jest jasne, czy stres prowadzi do problemów ze zdrowiem psychicznym, czy też osoby z problemami psychicznymi są bardziej podatne na stres. Może również istnieć trzecia zmienna, jak trudne warunki życiowe, które jednocześnie zwiększają poziom stresu i pogarszają zdrowie psychiczne.
Związek jest rzeczywisty, ale nie jest pewne, która zmienna wpływa na drugą, ani czy istnieje bezpośredni związek przyczynowo-skutkowy.
O związku przyczynowym, możemy mówić wtedy, gdy istnieje związek między zmiennymi, zachodzi odpowiedni porządek w czasie i wykluczyliśmy wszystkie inne alternatywne wyjaśnienia (np. kontrolując wpływ innych zmiennych oraz błędów próby).
Ustalenie wpływu wymaga zastosowania bardziej zaawansowanych metod badawczych, takich jak eksperymenty, które pozwalają na kontrolowanie zmiennych i wykluczenie alternatywnych wyjaśnień.
Kowariancja
Możesz kojarzyć również termin kowariancji. Aby rozjaśnić sytuację i uniknąć problemów chciałabym tylko szybko wskazać, że kowariancja jest po prostu niewystandaryzowaną miarą związku. To znaczy, że kowariancja również dostarczy informacji na temat zmiany, jakiej ulegnie zmienna B w związku ze zmianą zmiennej A. Minusem kowariancji jest jej zależność od skali pomiarowej i związany z tym brak możliwości określenia siły związku. Dlatego jest ona wykorzystywana rzadziej.
Wartość kowariancji może przyjmować dowolną liczbę rzeczywistą, co oznacza, że nie jest ograniczona do konkretnego przedziału. I trudniej ją zinterpretować
Właściwy współczynnik dla Ciebie
To, z jakiego współczynnika skorzystasz w swoim teście zależy od dwóch czynników. Po pierwsze od tego, na jakiej skali są Twoje zmienne (ilościowej, porządkowej czy nominalnej). Po drugie zaś od tego, czy Twoje dane spełniają dalsze założenia współczynników korelacji.
Wybierając należy pamiętać, że zależy nam na wyborze jak najsilniejszego współczynnika korelacji. Zawsze zaczynamy więc „od góry” – od rPearsona do C-kontyngencji.
W tabeli poniżej zilustrowałam wybór w zależności od skali pomiarowej zmiennych :
Tabela 1.
Wybór testu w zależności od skal pomiarowych
| Skala zmiennej 1 ilościowa | Skala zmiennej 2 porządkowa | nominalna | |
| ilościowa | r Pearsona | patrz: porządkowa x porządkowa | η (eta) |
| porządkowa | patrz: porządkowa x porządkowa | ρ Spearmana (rho) τ-b Kendalla (taub-b) τ-c Kendalla (tau-c) Gamma d Sommera | patrz: nominalna x nominalna |
| nominalna | η (eta) | patrz: nominalna x nominalna | φ Yula (phi) V Cramera C - kontyngencji |
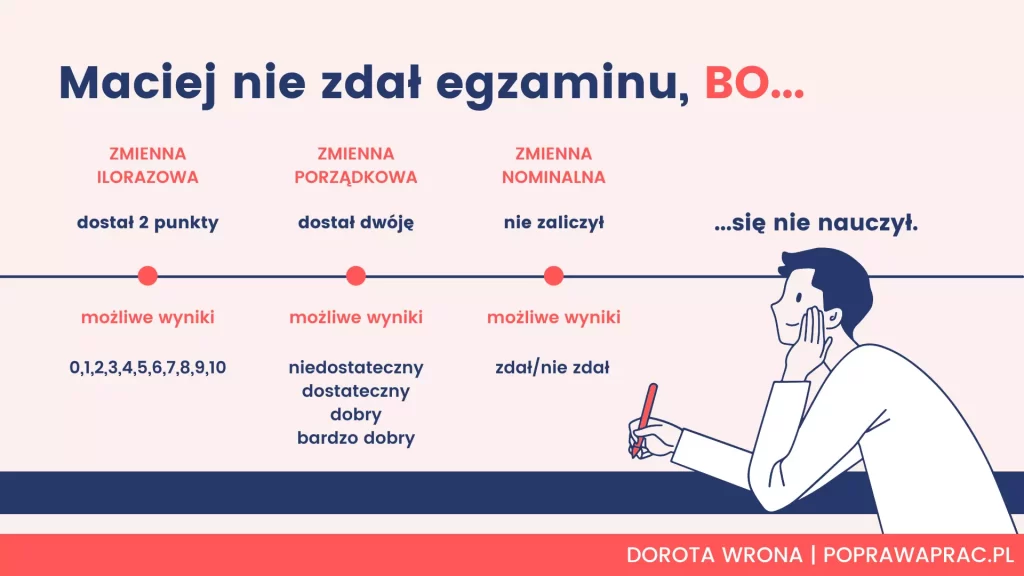
Krótkie wyjaśnienie skal pomiarowych:
- ilościowa posiada jednakowe przedziały oddzielające od siebie kolejne wartości zmiennej; przykłady: waga, wzrost, wynik w teście.
- porządkowa odległości pomiędzy kolejnymi wartościami nie są identyczne, ale określają hierarchię występowania; przykłady: wielkość miejsca zamieszkania, klasa samochodu.
- nominalna wartości tej zmiennej to etykiety, kategorie możliwych odpowiedzi; przykłady: płeć, kolor oczu, marka samochodu.
| Poniżej możesz zapoznać się ze szczegółowymi wymaganiami poszczególnych testów. |
Ilościowa x Ilościowa 𝑟 Pearsona
Zasadniczo rPearsona to jedyny parametryczny współczynnik korelacji. Traktuje się jako najlepszy współczynnik korelacji, najlepszy – ponieważ najbardziej godny zaufania. Jednak żeby móc w pełni skorzystać z jego możliwości, konieczne jest spełnienie rygorystycznych założeń:
- brak obserwacji odstających, czyli takich, które są znacznie powyżej lub poniżej ogólnej grupy. Przykład: kiedy badani ogólnie mają wyniki od 20 do 40, a jedna osoba posiada wynik 60;
- normalność rozkładu – zmienne, które chcemy skorelować, muszą mieć rozkład normalny;
- minimum 30 obserwacji (badanych).
Istnieją operacje statystyczne, które można wykonać (np. logarytmizacja), aby poradzić sobie z drobnymi problemami w spełnieniu założeń. Jednak kiedy nic nie pomaga – stosujemy ρ Spearmana.
Przykładowa hipoteza: Istnieje związek pomiędzy poziomem odczuwanego stresu a wynikiem w skali depresji.
Ilościowa x Nominalna η (eta)
W przypadku korelacji pomiędzy zmienną ilościową a nominalną (np. wzrost i płeć) możemy skorzystać z η. Jest to współczynnik, którego wynik przyjmuje wartość od 0 do 1, ale interpretacja pozostaje bez zmian. 0 oznacza brak związku, a im bliżej 1 – tym związek jest silniejszy.
Przykładowa hipoteza: Istnieje związek pomiędzy wzrostem a płcią.
Porządkowa x Porządkowa/Ilościowa
W każdym przypadku stosujemy je wtedy, gdy liczba wartości zmiennych wynosi przynajmniej 5. To znaczy, że jeżeli naszą zmienną jest wielkość miejsca zamieszkania, to musi ona mieć przynajmniej 5 wartości. Na przykład: wieś, miasteczko (do 20 tys.), małe miasto (20 – 150 tys.), miasto (150 – 500 tys.), duże miasto (powyżej 500 tys.).
Przykładowa hipoteza: Istnieje związek pomiędzy wielkością miejsca zamieszkania a poziomem odczuwanego stresu.
ρ Spearmana (rho)
Z ρ korzystamy zamiast r Pearsona. Jest współczynnikiem nieparametrycznym i mierzy zależność monotoniczną (również nieliniową). Jego zaletą jest również to, że nie jest tak wrażliwy na przypadki odstające i nie wymaga normalności rozkładu. Ale jednocześnie jego wyniki nie będą tak rzetelne, jak rPearsona. Stosujemy go wtedy, gdy liczba rang wiązanych jest mała (to znaczy, kiedy mamy dużą liczbę wartości dla obu zmiennych).
Przykładowa hipoteza: Istnieje związek pomiędzy poziomem odczuwanego stresu a wynikiem w skali depresji.
τ-b Kendalla (tau-b)
Również τ-b mierzy zależność monotoniczną. W odróżnieniu od ρ Spearmana stosujemy go wtedy, gdy liczba rang wiązanych jest duża (czyli wtedy, gdy mamy małą liczbę wartości obu zmiennych – 5 lub więcej).
Przykładowa hipoteza: Istnieje związek pomiędzy subiektywną oceną jakości życia a subiektywną oceną zdrowia.
τ-c Kendalla (tau-c)
Z kolei τ-c jest kolejnym współczynnikiem nieparametrycznym, który stosujemy wtedy, gdy zmienne znacznie różnią się liczbą przyjmowanych wartości. Na przykład jedna zmienna przyjmuje ich 5 (absolutne minimum) a druga – 50.
Przykładowa hipoteza: Istnieje związek pomiędzy subiektywną oceną jakości życia a wynikiem w skali depresji.
Gamma Kendalla
Gamma opiera się na analizie liczby par uporządkowanych zgodnie (gdzie większa wartość jednej zmiennej odpowiada większej wartości drugiej) oraz liczby par niezgodnych (gdzie relacje te są odwrotne).
Stosowany jest często w badaniach społecznych, psychologicznych i edukacyjnych, gdy analizowane są zależności między zmiennymi o charakterze porządkowym.
Gamma różni się od współczynnika korelacji Spearmana czy Pearsona tym, że kładzie większy nacisk na uporządkowanie rang, a nie na różnice pomiędzy wartościami zmiennych. Idealnie sprawdza się w analizie danych, gdzie wartości nie są dokładne liczbowo, ale można je uszeregować w sposób logiczny.
d Sommera
Z kolei d Sommera wykorzystujemy zamiast τ-b i ρ wtedy, gdy sądzimy, że analizowany związek jednak jest przyczynowo-skutkowy. Ostrożnie!
W przeciwieństwie do współczynnika gamma, który jest symetryczny, d Somersa jest asymetryczny. To oznacza, że możemy zdefiniować jedną zmienną jako zależną (Y), a drugą jako niezależną (X), co sprawia, że d Somersa jest bardziej użyteczny w analizie kierunkowych relacji.
Przykładowa hipoteza: Poziom zaangażowania pracowników (X) istotnie wpływa na poziom satysfakcji z pracy (Y).Nominalna x Nominalna/Porządkowa
φ Yula (phi)
Wykorzystujemy wtedy, gdy każda ze zmiennych przyjmuje 2 wartości. Na przykład gdy korelujemy płeć (kobieta/mężczyzna) i posiadanie kota (tak/nie).
Współczynnik φ (phi) Yule'a jest miarą siły zależności między dwiema zmiennymi nominalnymi, stosowaną w przypadku tabel kontyngencji 2x2 (czyli tabel, gdzie obie zmienne mają po dwie kategorie). Jest to specyficzna postać współczynnika korelacji Pearsona, jednakże ogranicza się do danych nominalnych, a dokładniej do przypadków dychotomicznych.
Przykładowa hipoteza: Istnieje istotna zależność między paleniem papierosów (zmienna nominalna) a wystąpieniem choroby serca (zmienna nominalna).
V Cramera
Współczynnik V Cramera jest miarą zależności między zmiennymi nominalnymi, stosowaną w przypadku tabel kontyngencji, w których przynajmniej jedna ze zmiennych ma więcej niż dwie kategorie (czyli dla tabel większych niż 2x2). Współczynnik V Cramera jest rozszerzeniem współczynnika φ (phi) Yule’a na większe tabele kontyngencji.
Można go wykorzystać, gdy zmienne mają różną ilość wartości . Na przykład płeć (kobieta/mężczyzna) oraz ulubiona marka samochodu (Opel/Škoda/Peugot/BMW/Nissan).
Przykładowa hipoteza: Istnieje związek pomiędzy ulubioną marką samochodu a płcią.
C-kontyngencji
Jest współczynnikiem wykorzystywanym w sytuacji, w której zmienne przyjmują taką samą ilość wartości. Na przykład ulubione zwierzątko (kot/pies/ptak/żółw/koń) oraz ulubiona marka samochodu (Opel/Škoda/Peugot/BMW/Nissan).
Przykładowa hipoteza: Istnieje związek pomiędzy ulubionym zwierzątkiem a ulubioną marką samochodu.
Nadal Potrzebujesz
POMOCY W PISANIU ?
Nazywam się Dorota Wrona. Moją misją jest pomoc studentom. Skorzystaj z ponad 25 lat doświadczenia w pisaniu i redakcji tekstów naukowych
Umów się na darmowe konsultacje

